首页 / 后端 / 文章

Collections与SkipListMap详解-黑马深入学习Java并发编程笔记

后端 潘老师 原 3周前 (03-31) 10 ℃ (0) 扫码查看

Collections

Collections类是用来操作集合的工具类，提供了集合转换成线程安全的方法：

 public static <T> Collection<T> synchronizedCollection(Collection<T> c) {
     return new SynchronizedCollection<>(c);
 }
public static <K,V> Map<K,V> synchronizedMap(Map<K,V> m) {
    return new SynchronizedMap<>(m);
}

源码：底层也是对方法进行加锁

public boolean add(E e) {
    synchronized (mutex) {return c.add(e);}
}

SkipListMap

底层结构

跳表 SkipList 是一个有序的链表，默认升序，底层是链表加多级索引的结构。跳表可以对元素进行快速查询，类似于平衡树，是一种利用空间换时间的算法
对于单链表，即使链表是有序的，如果查找数据也只能从头到尾遍历链表，所以采用链表上建索引的方式提高效率，跳表的查询时间复杂度是 O(logn)，空间复杂度 O(n)
ConcurrentSkipListMap 提供了一种线程安全的并发访问的排序映射表，内部是跳表结构实现，通过 CAS + volatile 保证线程安全
平衡树和跳表的区别：

  • 对平衡树的插入和删除往往很可能导致平衡树进行一次全局的调整；而对跳表的插入和删除，只需要对整个结构的局部进行操作
  • 在高并发的情况下，保证整个平衡树的线程安全需要一个全局锁；对于跳表则只需要部分锁，拥有更好的性能


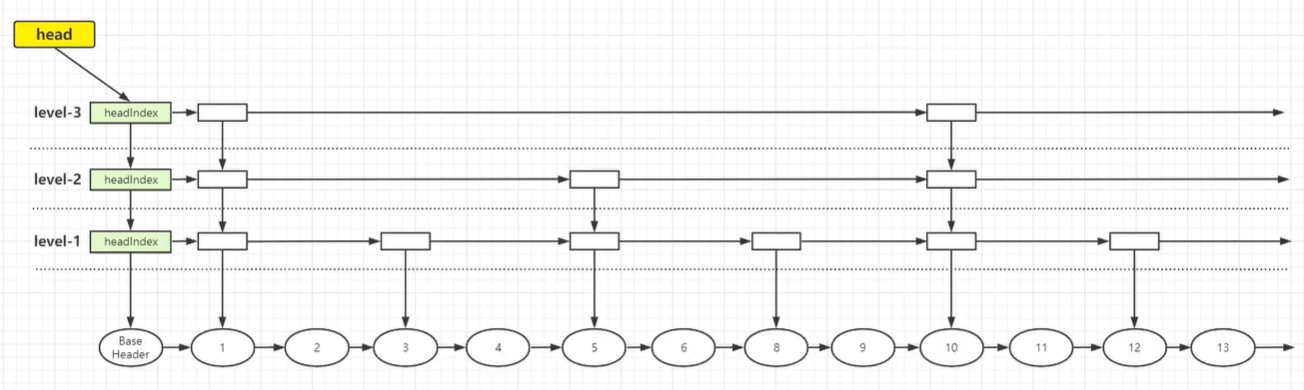
BaseHeader 存储数据，headIndex 存储索引，纵向上所有索引都指向链表最下面的节点

成员变量

  • 标识索引头节点位置 
    private static final Object BASE_HEADER = new Object();
  • 跳表的顶层索引 
    private transient volatile HeadIndex<K,V> head;
  • 比较器，为 null 则使用自然排序 
    final Comparator<? super K> comparator;
  • Node 节点 
    static final class Node<K, V>{
    final K key;                  // key 是 final 的, 说明节点一旦定下来, 除了删除, 一般不会改动 key
    volatile Object value;         // 对应的 value
    volatile Node<K, V> next;     // 下一个节点，单向链表
}
  • 索引节点 Index，只有向下和向右的指针 
    static class Index<K, V>{
    final Node<K, V> node;         // 索引指向的节点，每个都会指向数据节点
    final Index<K, V> down;     // 下边level层的Index，分层索引
    volatile Index<K, V> right; // 右边的Index，单向

    // 在 index 本身和 succ 之间插入一个新的节点 newSucc
    final boolean link(Index<K, V> succ, Index<K, V> newSucc){
        Node<K, V> n = node;
        newSucc.right = succ;
        // 把当前节点的右指针从 succ 改为 newSucc
        return n.value != null && casRight(succ, newSucc);
    }

    // 断开当前节点和 succ 节点，将当前的节点 index 设置其的 right 为 succ.right，就是把 succ 删除
    final boolean unlink(Index<K, V> succ){
        return node.value != null && casRight(succ, succ.right);
    }
}
  • 头索引节点 HeadIndex 
    static final class HeadIndex<K,V> extends Index<K,V> {
    final int level;    // 表示索引层级，所有的 HeadIndex 都指向同一个 Base_header 节点
    HeadIndex(Node<K,V> node, Index<K,V> down, Index<K,V> right, int level) {
        super(node, down, right);
        this.level = level;
    }
}

成员方法

其他方法
  • 构造方法： 
    public ConcurrentSkipListMap() {
    this.comparator = null;    // comparator 为 null，使用 key 的自然序，如字典序
    initialize();
}

    private void initialize() {
    keySet = null;
    entrySet = null;
    values = null;
    descendingMap = null;
    // 初始化索引头节点，Node 的 key 为 null，value 为 BASE_HEADER 对象，下一个节点为 null
    // head 的分层索引 down 为 null，链表的后续索引 right 为 null，层级 level 为第 1 层
    head = new HeadIndex<K,V>(new Node<K,V>(null, BASE_HEADER, null), null, null, 1);
}
  • cpr：排序 
    //　x 是比较者，y 是被比较者，比较者大于被比较者 返回正数，小于返回负数，相等返回 0
static final int cpr(Comparator c, Object x, Object y) {
    return (c != null) ? c.compare(x, y) : ((Comparable)x).compareTo(y);
}
添加方法
  • findPredecessor()：寻找前置节点
    从最上层的头索引开始向右查找（链表的后续索引），如果后续索引的节点的 key 大于要查找的 key，则头索引移到下层链表，在下层链表查找，以此反复，一直查找到没有下层的分层索引为止，返回该索引的节点。如果后续索引的节点的 key 小于要查找的 key，则在该层链表中向后查找。由于查找的 key 可能永远大于索引节点的 key，所以只能找到目标的前置索引节点。如果遇到空值索引的存在，通过 CAS 来断开索引

    private Node<K,V> findPredecessor(Object key, Comparator<? super K> cmp) {
    if (key == null)
        throw new NullPointerException(); // don't postpone errors
    for (;;) {
        // 1.初始数据 q 是 head，r 是最顶层 h 的右 Index 节点
        for (Index<K,V> q = head, r = q.right, d;;) {
            // 2.右索引节点不为空，则进行向下查找
            if (r != null) {
                Node<K,V> n = r.node;
                K k = n.key;
                // 3.n.value 为 null 说明节点 n 正在删除的过程中，此时【当前线程帮其删除索引】
                if (n.value == null) {
                    // 在 index 层直接删除 r 索引节点
                    if (!q.unlink(r))
                        // 删除失败重新从 head 节点开始查找，break 一个 for 到步骤 1，又从初始值开始
                        break;
                    
                    // 删除节点 r 成功，获取新的 r 节点,
                    r = q.right;
                    // 回到步骤 2，还是从这层索引开始向右遍历
                    continue;
                }
                // 4.若参数 key > r.node.key，则继续向右遍历, continue 到步骤 2 处获取右节点
                //   若参数 key < r.node.key，说明需要进入下层索引，到步骤 5
                if (cpr(cmp, key, k) > 0) {
                    q = r;
                    r = r.right;
                    continue;
                }
            }
            // 5.先让 d 指向 q 的下一层，判断是否是 null，是则说明已经到了数据层，也就是第一层
            if ((d = q.down) == null) 
                return q.node;
            // 6.未到数据层, 进行重新赋值向下扫描
            q = d;        // q 指向 d
            r = d.right;// r 指向 q 的后续索引节点，此时(q.key < key < r.key)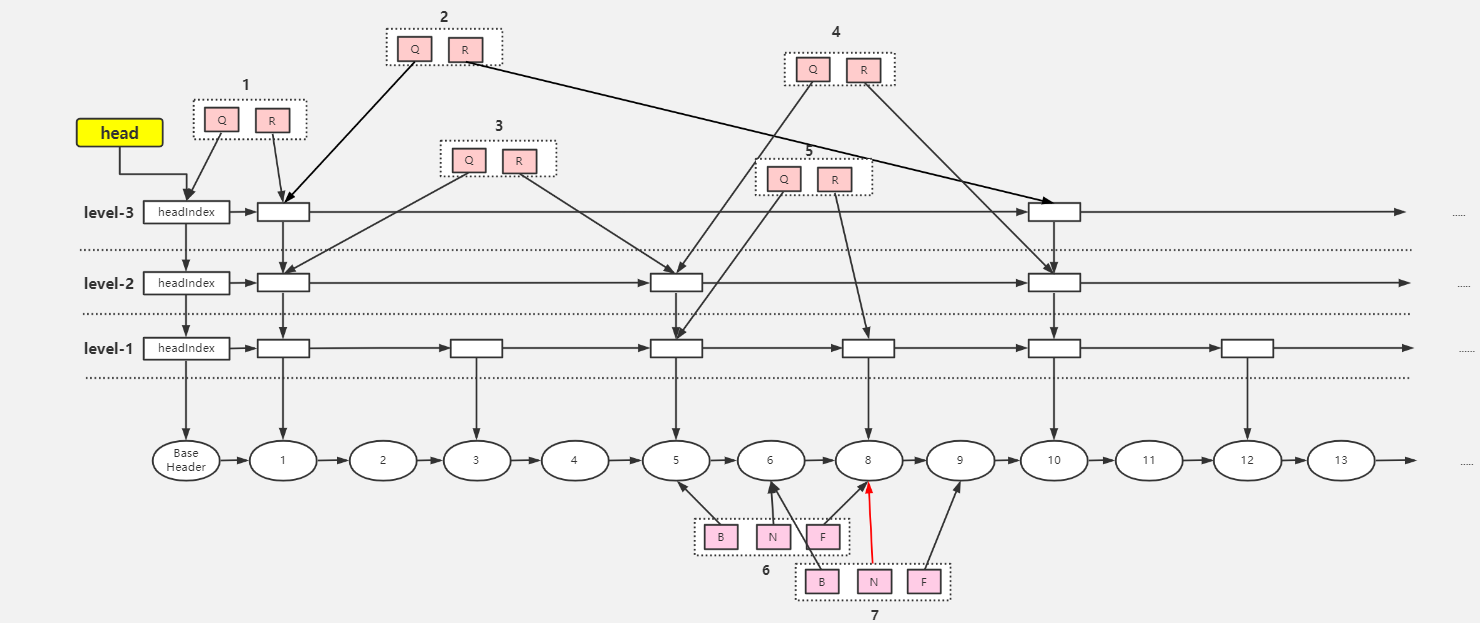
        }
    }
}

  • put()：添加数据 
    public V put(K key, V value) {
    // 非空判断，value不能为空
    if (value == null)
        throw new NullPointerException();
    return doPut(key, value, false);
}

    private V doPut(K key, V value, boolean onlyIfAbsent) {
Node<K,V> z;
// 非空判断，key 不能为空
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
// outer 循环，【把待插入数据插入到数据层的合适的位置，并在扫描过程中处理已删除(value = null)的数据】
outer: for (;;) {
//0.for (;;)
//1.将 key 对应的前继节点找到, b 为前继节点，是数据层的, n 是前继节点的 next, 
//  若没发生条件竞争，最终 key 在 b 与 n 之间 (找到的 b 在 base_level 上)
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
// 2.n 不为 null 说明 b 不是链表的最后一个节点
if (n != null) {
Object v; int c;
// 3.获取 n 的右节点
Node<K,V> f = n.next;
// 4.条件竞争，并发下其他线程在 b 之后插入节点或直接删除节点 n, break 到步骤 0
if (n != b.next)              
break;
//  若节点 n 已经删除, 则调用 helpDelete 进行【帮助删除节点】
if ((v = n.value) == null) {
n.helpDelete(b, f);
break;
}
// 5.节点 b 被删除中，则 break 到步骤 0,
//  【调用findPredecessor帮助删除index层的数据, node层的数据会通过helpDelete方法进行删除】
if (b.value == null || v == n) 
break;
// 6.若 key > n.key，则进行向后扫描
//   若 key < n.key，则证明 key 应该存储在 b 和 n 之间
if ((c = cpr(cmp, key, n.key)) > 0) {
b = n;
n = f;
continue;
}
// 7.key 的值和 n.key 相等，则可以直接覆盖赋值
if (c == 0) {
// onlyIfAbsent 默认 false，
if (onlyIfAbsent || n.casValue(v, value)) {
@SuppressWarnings("unchecked") V vv = (V)v;
// 返回被覆盖的值
return vv;
}
// cas失败，break 一层循环，返回 0 重试
break;
}
// else c < 0; fall through
}
// 8.此时的情况 b.key < key < n.key，对应流程图1中的7，创建z节点指向n
z = new Node<K,V>(key, value, n);
// 9.尝试把 b.next 从 n 设置成 z
if (!b.casNext(n, z))
// cas失败，返回到步骤0，重试
break;
// 10.break outer 后, 上面的 for 循环不会再执行, 而后执行下面的代码
break outer;
}
}
// 【以上插入节点已经完成，剩下的任务要根据随机数的值来表示是否向上增加层数与上层索引】
// 随机数
int rnd = ThreadLocalRandom.nextSecondarySeed();
// 如果随机数的二进制与 10000000000000000000000000000001 进行与运算为 0
// 即随机数的二进制最高位与最末尾必须为 0，其他位无所谓，就进入该循环
// 如果随机数的二进制最高位与最末位不为 0，不增加新节点的层数
// 11.判断是否需要添加 level，32 位
if ((rnd & 0x80000001) == 0) {
// 索引层 level，从 1 开始，就是最底层
int level = 1, max;
// 12.判断最低位前面有几个 1，有几个leve就加几：0..0 0001 1110，这是4个，则1+4=5
//    【最大有30个就是 1 + 30 = 31
while (((rnd >>>= 1) & 1) != 0)
++level;
// 最终会指向 z 节点，就是添加的节点 
Index<K,V> idx = null;
// 指向头索引节点
HeadIndex<K,V> h = head;
// 13.判断level是否比当前最高索引小，图中 max 为 3
if (level <= (max = h.level)) {
for (int i = 1; i <= level; ++i)
// 根据层数level不断创建新增节点的上层索引，索引的后继索引留空
// 第一次idx为null，也就是下层索引为空，第二次把上次的索引作为下层索引，【类似头插法】
idx = new Index<K,V>(z, idx, null);
// 循环以后的索引结构
// index-3    ← idx
//   ↓
// index-2
//   ↓
// index-1
//   ↓
//  z-node
}
// 14.若 level > max，则【只增加一层 index 索引层】，3 + 1 = 4
else { 
level = max + 1;
//创建一个 index 数组，长度是 level+1，假设 level 是 4，创建的数组长度为 5
Index<K,V>[] idxs = (Index<K,V>[])new Index<?,?>[level+1];
// index[0]的数组 slot 并没有使用，只使用 [1,level] 这些数组的 slot
for (int i = 1; i <= level; ++i)
idxs[i] = idx = new Index<K,V>(z, idx, null);
// index-4   ← idx
//   ↓
// ......
//   ↓
// index-1
//   ↓
//  z-node
for (;;) {
h = head;
// 获取头索引的层数，3
int oldLevel = h.level;
// 如果 level <= oldLevel，说明其他线程进行了 index 层增加操作，退出循环
if (level <= oldLevel)
break;
// 定义一个新的头索引节点
HeadIndex<K,V> newh = h;
// 获取头索引的节点，就是 BASE_HEADER
Node<K,V> oldbase = h.node;
// 升级 baseHeader 索引，升高一级，并发下可能升高多级
for (int j = oldLevel + 1; j <= level; ++j)
// 参数1：底层node，参数二：down，为以前的头节点，参数三：right，新建
newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);
// 执行完for循环之后，baseHeader 索引长这个样子，这里只升高一级
// index-4             →             index-4    ← idx
//   ↓                                  ↓
// index-3                           index-3     
//   ↓                                  ↓
// index-2                           index-2
//   ↓                                  ↓
// index-1                           index-1
//   ↓                                  ↓
// baseHeader    →    ....      →     z-node
// cas 成功后，head 字段指向最新的 headIndex，baseHeader 的 index-4
if (casHead(h, newh)) {
// h 指向最新的 index-4 节点
h = newh;
// 让 idx 指向 z-node 的 index-3 节点，
// 因为从 index-3 - index-1 的这些 z-node 索引节点 都没有插入到索引链表
idx = idxs[level = oldLevel];
break;
}
}
}
// 15.【把新加的索引插入索引链表中】，有上述两种情况，一种索引高度不变，另一种是高度加 1
// 要插入的是第几层的索引
splice: for (int insertionLevel = level;;) {
// 获取头索引的层数，情况 1 是 3，情况 2 是 4
int j = h.level;
// 【遍历 insertionLevel 层的索引，找到合适的插入位置】
for (Index<K,V> q = h, r = q.right, t = idx;;) {
// 如果头索引为 null 或者新增节点索引为 null，退出插入索引的总循环
if (q == null || t == null)
// 此处表示有其他线程删除了头索引或者新增节点的索引
break splice;
// 头索引的链表后续索引存在，如果是新层则为新节点索引，如果是老层则为原索引
if (r != null) {
// 获取r的节点
Node<K,V> n = r.node;
// 插入的key和n.key的比较值
int c = cpr(cmp, key, n.key);
// 【删除空值索引】
if (n.value == null) {
if (!q.unlink(r))
break;
r = q.right;
continue;
}
// key > r.node.key，向右扫描
if (c > 0) {
q = r;
r = r.right;
continue;
}
}
// 执行到这里，说明 key < r.node.key，判断是否是第 j 层插入新增节点的前置索引
if (j == insertionLevel) {
// 【将新索引节点 t 插入 q r 之间】
if (!q.link(r, t))
break; 
// 如果新增节点的值为 null，表示该节点已经被其他线程删除
if (t.node.value == null) {
// 找到该节点
findNode(key);
break splice;
}
// 插入层逐层自减，当为最底层时退出循环
if (--insertionLevel == 0)
break splice;
}
// 其他节点随着插入节点的层数下移而下移
if (--j >= insertionLevel && j < level)
t = t.down;
q = q.down;
r = q.right;
}
}
}
return null;
}
  • findNode() 
    private Node<K,V> findNode(Object key) {
// 原理与doGet相同，无非是 findNode 返回节点，doGet 返回 value
if ((c = cpr(cmp, key, n.key)) == 0)
return n;
}
获取方法
  • get(key)：获取对应的数据 
    public V get(Object key) {
return doGet(key);
}
  • doGet()：扫描过程会对已 value = null 的元素进行删除处理 
    private V doGet(Object key) {
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {
// 1.找到最底层节点的前置节点
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
Object v; int c;
// 2.【如果该前置节点的链表后续节点为 null，说明不存在该节点】
if (n == null)
break outer;
// b → n → f
Node<K,V> f = n.next;
// 3.如果n不为前置节点的后续节点，表示已经有其他线程删除了该节点
if (n != b.next) 
break;
// 4.如果后续节点的值为null，【需要帮助删除该节点】
if ((v = n.value) == null) {
n.helpDelete(b, f);
break;
}
// 5.如果前置节点已被其他线程删除，重新循环
if (b.value == null || v == n)
break;
// 6.如果要获取的key与后续节点的key相等，返回节点的value
if ((c = cpr(cmp, key, n.key)) == 0) {
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
// 7.key < n.key，因位 key > b.key，b 和 n 相连，说明不存在该节点或者被其他线程删除了
if (c < 0)
break outer;
b = n;
n = f;
}
}
return null;
}
删除方法
  • remove() 
    public V remove(Object key) {
return doRemove(key, null);
}
final V doRemove(Object key, Object value) {
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {
// 1.找到最底层目标节点的前置节点，b.key < key
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
Object v; int c;
// 2.如果该前置节点的链表后续节点为 null，退出循环，说明不存在这个元素
if (n == null)
break outer;
// b → n → f
Node<K,V> f = n.next;
if (n != b.next)                    // inconsistent read
break;
if ((v = n.value) == null) {        // n is deleted
n.helpDelete(b, f);
break;
}
if (b.value == null || v == n)      // b is deleted
break;
//3.key < n.key，说明被其他线程删除了，或者不存在该节点
if ((c = cpr(cmp, key, n.key)) < 0)
break outer;
//4.key > n.key，继续向后扫描
if (c > 0) {
b = n;
n = f;
continue;
}
//5.到这里是 key = n.key，value 不为空的情况下判断 value 和 n.value 是否相等
if (value != null && !value.equals(v))
break outer;
//6.【把 n 节点的 value 置空】
if (!n.casValue(v, null))
break;
//7.【给 n 添加一个删除标志 mark】，mark.next = f，然后把 b.next 设置为 f，成功后n出队
if (!n.appendMarker(f) || !b.casNext(n, f))
// 对 key 对应的 index 进行删除，调用了 findPredecessor 方法
findNode(key);
else {
// 进行操作失败后通过 findPredecessor 中进行 index 的删除
findPredecessor(key, cmp);
if (head.right == null)
// 进行headIndex 对应的index 层的删除
tryReduceLevel();
}
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
}
return null;
}

    经过 findPredecessor() 中的 unlink() 后索引已经被删除

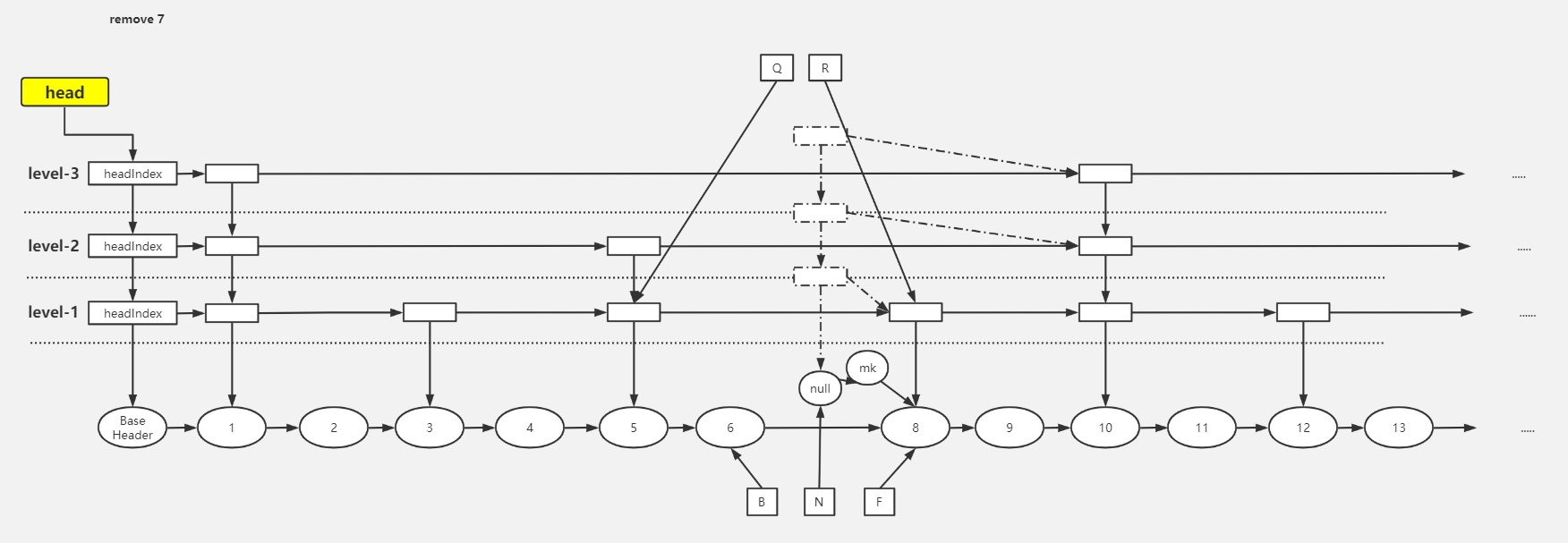
  • appendMarker()：添加删除标记节点 
    boolean appendMarker(Node<K,V> f) {
// 通过 CAS 让 n.next 指向一个 key 为 null，value 为 this，next 为 f 的标记节点
return casNext(f, new Node<K,V>(f));
}
  • helpDelete()：将添加了删除标记的节点清除，参数是该节点的前驱和后继节点 
    void helpDelete(Node<K,V> b, Node<K,V> f) {
// this 节点的后续节点为 f，且本身为 b 的后续节点，一般都是正确的，除非被别的线程删除
if (f == next && this == b.next) {
// 如果 n 还还没有被标记
if (f == null || f.value != f) 
casNext(f, new Node<K,V>(f));
else
// 通过 CAS，将 b 的下一个节点 n 变成 f.next，即成为图中的样式
b.casNext(this, f.next);
}
}
  • tryReduceLevel()：删除索引 
    private void tryReduceLevel() {
HeadIndex<K,V> h = head;
HeadIndex<K,V> d;
HeadIndex<K,V> e;
if (h.level > 3 &&
(d = (HeadIndex<K,V>)h.down) != null &&
(e = (HeadIndex<K,V>)d.down) != null &&
e.right == null &&
d.right == null &&
h.right == null &&
// 设置头索引
casHead(h, d) && 
// 重新检查
h.right != null) 
// 重新检查返回true，说明其他线程增加了索引层级，把索引头节点设置回来
casHead(d, h);   
}

参考文章：https://my.oschina.net/u/3768341/blog/3135659
参考视频：https://www.bilibili.com/video/BV1Er4y1P7k1

版权声明：本站文章，如无说明，均为本站原创，转载请注明文章来源。如有侵权，请联系博主删除。
本文链接：https://www.panziye.com/back/16633.html
喜欢 (0)赏
【请潘老师喝杯Coffee吧！】
分享 (0)

相关文章

用户头像
发表我的评论
取消评论
表情 贴图 签到 代码

Hi，您需要填写昵称和邮箱！

  • 昵称【必填】
  • 邮箱【必填】
  • 网址【可选】